Funktion, in der Mathematik ein Ausdruck, eine Regel oder ein Gesetz, das eine Beziehung zwischen einer Variablen (der unabhängigen Variablen) und einer anderen Variablen (der abhängigen Variablen) definiert.
Was ist eine Funktion in der Mathematik?
Funktion, in der Mathematik ein Ausdruck, eine Regel oder ein Gesetz, das eine Beziehung zwischen einer Variablen (der unabhängigen Variablen) und einer anderen Variablen (der abhängigen Variablen) definiert.
Was ist eine Funktion in einfacher Definition?
Eine Funktion ist definiert als eine Beziehung zwischen einer Reihe von Eingaben mit jeweils einer Ausgabe. Einfach ausgedrückt ist eine Funktion eine Beziehung zwischen Eingaben, wobei jede Eingabe mit genau einer Ausgabe verknüpft ist. Jede Funktion hat eine Domäne und eine Kodomäne oder einen Bereich.
WAS IST Funktion und Beispiel?
Eine Funktion ist eine Art Regel, die für eine Eingabe eine Ausgabe liefert. Bildquelle: von Alex Federspiel. Ein Beispiel hierfür wäre y=x2. Wenn Sie etwas für x eingeben, erhalten Sie eine Ausgabe für y. Wir würden sagen, dass y eine Funktion von x ist, da x der Eingabewert ist.
Was sind Funktionen in der Algebra?
Eine Funktion verknüpft einen Eingang mit einem Ausgang. Es ist wie eine Maschine, die einen Eingang und einen Ausgang hat. Und der Output hängt irgendwie mit dem Input zusammen. f(x) „f(x) = … “ ist die klassische Schreibweise einer Funktion.
Was ist eine Funktion in Mathematik?
Funktion, in der Mathematik ein Ausdruck, eine Regel oder ein Gesetz, das eine Beziehung zwischen einer Variablen (der unabhängigen Variablen) und einer anderen Variablen (der abhängigen Variablen) definiert.
Was ist eine Funktion in einfacher Definition?
Eine Funktion ist definiert als eine Beziehung zwischen einer Reihe von Eingaben mit jeweils einer Ausgabe. Einfach ausgedrückt ist eine Funktion eine Beziehung zwischen Eingaben, wobei jede Eingabe mit genau einer Ausgabe verknüpft ist. Jede Funktion hat eine Domäne und eine Kodomäne oder einen Bereich.
Was sindFunktionen in der Algebra?
Eine Funktion verknüpft einen Eingang mit einem Ausgang. Es ist wie eine Maschine, die einen Eingang und einen Ausgang hat. Und der Output hängt irgendwie mit dem Input zusammen. f(x) „f(x) = … “ ist die klassische Schreibweise einer Funktion.
Wie erkennen Sie, dass es sich um eine Funktion handelt?
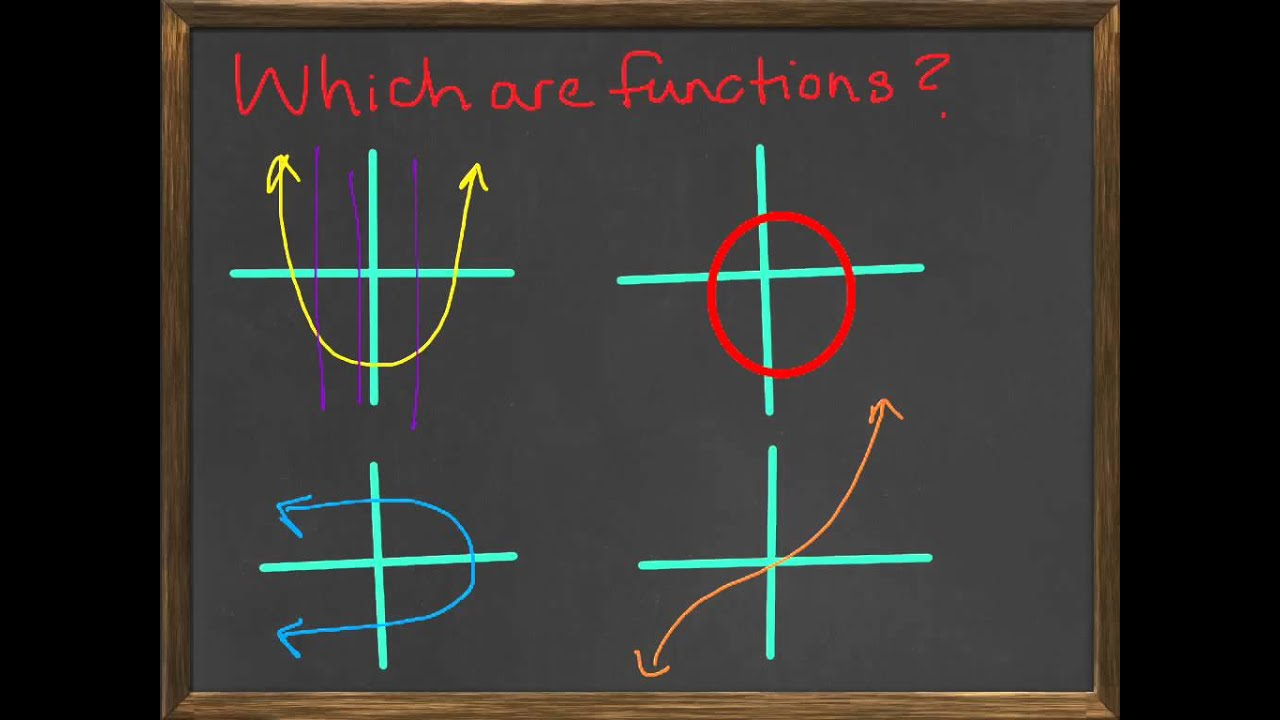
Untersuchen Sie das Diagramm, um festzustellen, ob eine vertikale Linie die Kurve mehr als einmal schneidet. Wenn es eine solche Linie gibt, stellt der Graph keine Funktion dar. Wenn keine vertikale Linie die Kurve mehr als einmal schneiden kann, stellt der Graph eine Funktion dar.
Woran erkennen Sie, dass es sich um eine Funktion handelt?
Verwenden Sie den vertikalen Linientest, um festzustellen, ob ein Diagramm eine Funktion darstellt oder nicht. Wenn eine vertikale Linie über den Graphen bewegt wird und den Graphen zu irgendeinem Zeitpunkt nur an einem Punkt berührt, dann ist der Graph eine Funktion. Wenn die vertikale Linie den Graphen an mehr als einem Punkt berührt, dann ist der Graph keine Funktion.
Was ist keine Funktion?
Senkrechte Linien sind keine Funktionen. Die Gleichungen y = ± x und x 2 + y 2 = 9 sind Beispiele für Nichtfunktionen, weil es mindestens einen -Wert mit zwei oder mehr -Werten gibt.
Welche Arten von Funktionen gibt es?
Arten von Funktionen Viele – eine Funktion. Onto – Funktion (Surjektive Funktion) Into – Funktion. Polynomfunktion.
Welche Gleichung ist keine Funktion?
Senkrechte Linien sind keine Funktionen. Die Gleichungen y = ± x und x 2 + y 2 = 9 sind Beispiele für Nichtfunktionen, weil es mindestens einen -Wert mit zwei oder mehr -Werten gibt.
Was ist der Unterschied zwischen einer Funktion und einer Gleichung?
Eine Funktion hat mindestens 2 Variablen: eine Ausgangsvariable und eine oder mehrere Eingangsvariablen. Eine Gleichung besagt, dass zwei Ausdrücke gleich sind, und sie kann eine beliebige Anzahl von Variablen beinhalten (keine, eine oder mehr). Eine Funktion kann oft als geschrieben werdenGleichung, aber nicht jede Gleichung ist eine Funktion.
Was ist die beste Definition für Funktion?
Eine technische Definition einer Funktion ist: eine Beziehung von einer Menge von Eingaben zu einer Menge möglicher Ausgaben, wobei jede Eingabe genau einer Ausgabe zugeordnet ist.
Was ist eine Funktionsdefinition für Kinder?
Funktion. • eine mathematische Beziehung zwischen einer Menge von Eingaben und einer Menge von Ausgaben. • Der Ausgangswert hängt vom Eingangswert ab (ist eine Funktion davon). und jede Eingabe erzeugt genau eine Ausgabe.
Was ist eine Funktion in Mathematik?
Funktion, in der Mathematik ein Ausdruck, eine Regel oder ein Gesetz, das eine Beziehung zwischen einer Variablen (der unabhängigen Variablen) und einer anderen Variablen (der abhängigen Variablen) definiert.
Was ist eine Funktion in einfacher Definition?
Eine Funktion ist definiert als eine Beziehung zwischen einer Reihe von Eingaben mit jeweils einer Ausgabe. Einfach ausgedrückt ist eine Funktion eine Beziehung zwischen Eingaben, wobei jede Eingabe mit genau einer Ausgabe verknüpft ist. Jede Funktion hat eine Domäne und eine Kodomäne oder einen Bereich.
Was sind Funktionen in der Algebra?
Eine Funktion verknüpft einen Eingang mit einem Ausgang. Es ist wie eine Maschine, die einen Eingang und einen Ausgang hat. Und der Output hängt irgendwie mit dem Input zusammen. f(x) „f(x) = … “ ist die klassische Schreibweise einer Funktion.
Warum ist es eine Funktion?
Eine Funktion ist eine Beziehung, bei der jeder Eingang nur einen Ausgang hat. In der Relation ist y eine Funktion von x, weil es für jede Eingabe x (1, 2, 3 oder 0) nur eine Ausgabe y gibt. x ist keine Funktion von y, weil die Eingabe y = 3 mehrere Ausgaben hat: x = 1 und x = 2.
WAS IST Funktion und Nichtfunktion?
Was ist der Unterschied zwischen funktionalen und nicht funktionalen Anforderungen? Funktionale Anforderungen erklären, wie das System funktionieren muss, während nichtfunktionale Anforderungen erklären, wie das System funktioniertdurchführen sollte.
Wie viele Typen sind Funktionen?
Die Arten von Funktionen können grob in vier Typen eingeteilt werden. Basierend auf Element: Eins-zu-eins-Funktion, viele-zu-eins-Funktion, auf Funktion, eins-zu-eins und auf Funktion, in Funktion. Basierend auf Domain: Algebraische Funktionen, Trigonometriefunktionen, logarithmische Funktionen.