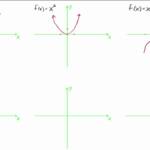
Zu den Hauptmerkmalen gehören: Intercepts; Intervalle, in denen die Funktion zunimmt, abnimmt, positiv oder negativ ist; relative Maxima und Minima; Symmetrien; EndverhaltenEndverhaltenDas Endverhalten einer Funktion f beschreibt das Verhalten des Graphen der Funktion an den „Enden“ der x-Achse. Mit anderen Worten, das Endverhalten einer Funktion beschreibt den Trend des Graphen, wenn wir zum rechten Ende der x-Achse (wenn x sich +∞ nähert) und zum linken Ende der x-Achse (wenn x sich − nähert) blicken ∞ ).https://www.khanacademy.org › Endverhalten-von-PolynomenEndverhalten von Polynomen (Artikel)
Das ist so ziemlich alles, was es zu „Operationen mit Funktionen“ zu tun gibt, bis Sie zur Funktionskomposition kommen. Lassen Sie sich von der Notation für dieses Thema nicht beunruhigen; es bedeutet nichts anderes als genau das, was es sagt: addieren, subtrahieren, multiplizieren oder dividieren; dann vereinfachen und nach Bedarf auswerten.
Wie definiert man eine Funktion?
Funktion, in der Mathematik ein Ausdruck, eine Regel oder ein Gesetz, das eine Beziehung zwischen einer Variablen (der unabhängigen Variablen) und einer anderen Variablen (der abhängigen Variablen) definiert.
Was ist die Form einer Funktion?
Eine Gleichung mit x und y, die auch eine Funktion ist, kann in der Form y = „ein Ausdruck mit x“ geschrieben werden; das heißt, y = f ( x). Dieser letzte Ausdruck wird gelesen als „y ist gleich f von x“ und bedeutet, dass y eine Funktion von x ist.
Was ist die Grundform der Funktion?
Einfachste Form oder allgemein geschriebene Regel einer Funktion, die keine Parameter enthält. Einige Autoren verwenden stattdessen den Begriff „Basisfunktion“.
Was sind die zwei wichtigen Teile einer Funktion?
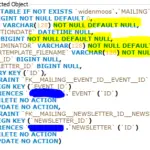
Eine Funktionsdefinition besteht aus zwei Hauptkomponenten: der ersten Zeile (einschließlich der Argumentdeklarationen) und dem sogenannten Hauptteil der Funktion. Die zulässigen Datentypen für die Argumente einer Funktion sind int und double.
Wie heißen die Teile einer Funktion?
Eingabe, Beziehung, Ausgabe Wir werden viele Möglichkeiten sehen, über Funktionen nachzudenken, aber es gibt immer drei Hauptteile: Die Eingabe. Die Beziehung. Die Ausgabe.
Was sind die 8 Grundfunktionen?
Die acht Typen sind linear, Potenz, quadratisch, polynomisch, rational, exponentiell, logarithmisch und sinusförmig.
Was sind Funktionstypen?
Arten von Funktionen – basierend auf Gleichung Konstante Funktion: Die Polynomfunktion vom Grad Null. Lineare Funktion: Die Polynomfunktion ersten Grades.Quadratische Funktion: Die Polynomfunktion zweiten Grades. Kubische Funktion: Die Polynomfunktion dritten Grades.
Was sind die sechs Funktionen?
Betriebsplanung Überwachung der täglichen Warenproduktion. Verwaltung und Kontrolle Ihres Inventars. Behalten Sie die Leistung und das Wohlbefinden der Teammitglieder im Auge. Produktionsplanung.
Was sind die 4 Reihenfolgen der Operationen?
Wir können uns die Reihenfolge mit PEMDAS merken: Klammern, Exponenten, Multiplikation und Division (von links nach rechts), Addition und Subtraktion (von links nach rechts).
Welches ist ein Beispiel für eine Funktion?
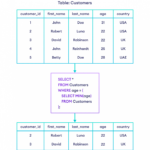
Wir könnten eine Funktion definieren, bei der die Domäne X wieder die Menge der Personen ist, aber die Codomain eine Menge von Zahlen ist. Nehmen wir zum Beispiel an, dass die Kodomäne Y die Menge ganzer Zahlen ist, und definieren Sie die Funktion c so, dass für jede Person x die Funktionsausgabe c(x) die Anzahl der Kinder der Person x ist.
Was ist eine Eins-Eins-Funktion?
In der Mathematik ist eine injektive Funktion oder Injektion oder Eins-Eins-Funktion eine Funktion, die Individualität umfasst, die niemals diskrete Elemente ihrer Domäne auf das äquivalente Element ihrer Kodomäne abbildet. Wir können sagen, dass jedes Element der Kodomäne das Abbild nur eines Elements seiner Domäne ist.
Was definiert Funktion?
Eine technische Definition einer Funktion ist: eine Beziehung von einer Menge von Eingaben zu einer Menge möglicher Ausgaben, wobei jede Eingabe genau einer Ausgabe zugeordnet ist.
Was nennt man eine Funktion?
Funktion, in der Mathematik ein Ausdruck, eine Regel oder ein Gesetz, das eine Beziehung zwischen einer Variablen (der unabhängigen Variablen) und einer anderen Variablen (der abhängigen Variablen) definiert.
Wie funktionieren Funktionen?
Eine Funktion ist eine Gleichung, die nur eine Antwort für y für jedes x hat. Eine Funktion weist jedem Eingang eines bestimmten Typs genau einen Ausgang zu. es istEs ist üblich, eine Funktion entweder f(x) oder g(x) anstelle von y zu nennen. f(2) bedeutet, dass wir den Wert unserer Funktion finden sollten, wenn x gleich 2 ist.
Was haben alle Funktionen gemeinsam?
Eine Funktion ist eine Relation, bei der jeder mögliche Eingabewert zu genau einem Ausgabewert führt. Wir sagen „der Output ist eine Funktion des Inputs“. Die Eingabewerte bilden die Domäne und die Ausgabewerte den Bereich.
Was sind die zwei Haupttypen von Funktionen?
2. Was sind die zwei Haupttypen von Funktionen? Erläuterung: Integrierte und benutzerdefinierte Funktionen.