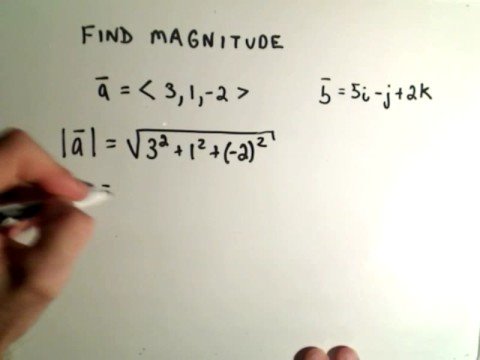einfacher anzuwenden als Geometrie und erfordert die Kenntnis weniger Regeln. Die Mechanik der Vektoralgebra ist unkompliziert und erfordert weniger Intuition und Cleverness beim Finden einer Lösung.
Was bedeutet Vektoralgebra?
: eine Algebra, bei der die beteiligten Elemente Vektoren darstellen können und die Annahmen und Regeln auf dem Verhalten von Vektoren basieren.
Was ist ein Vektor in der Mathematik?
Vektor, in der Mathematik eine Größe, die sowohl Größe als auch Richtung, aber keine Position hat. Beispiele für solche Größen sind Geschwindigkeit und Beschleunigung.
Wie schreibt man einen Vektor?
Wenn ein Vektor nur eine Liste von Zahlen ist, können wir ihn uns als Pfeil im Raum vorstellen. Zum Beispiel stellen wir uns den Vektor (4,2)left parenthesis, 4, comma, 2, right parenthesis als einen Pfeil vor, dessen Ende am Ursprung und dessen Spitze am Punkt ( 4 , 2 ) (4, 2) ( 4,2)linke Klammer, 4, Komma, 2, rechte Klammer.
Wie untersucht man Vektoren?
Sie können die Größe eines Vektors in drei Dimensionen finden, indem Sie die Formel a2=b2+c2+d2 verwenden, wobei a die Größe des Vektors ist und b, c und d die Komponenten in jeder Richtung sind. Das Kreuzprodukt von Vektoren ist nicht kommutativ. Kollineare Vektoren sind auch parallele Vektoren, außer dass sie auf derselben Linie liegen.
Wie schreibt man einen Vektor?
Wenn ein Vektor nur eine Liste von Zahlen ist, können wir ihn uns als Pfeil im Raum vorstellen. Zum Beispiel stellen wir uns den Vektor (4,2)left parenthesis, 4, comma, 2, right parenthesis als einen Pfeil vor, dessen Ende am Ursprung und dessen Spitze am Punkt ( 4 , 2 ) (4, 2) ( 4,2)linke Klammer, 4, Komma, 2, rechte Klammer.
Wie sieht ein Vektor aus?
Definition eines Vektors. Ein Vektor ist ein Objekt, das sowohl eine Größe als auch eine Richtung hat. Geometrisch können wir uns einen Vektor als gerichtet vorstellenLiniensegment, dessen Länge der Betrag des Vektors ist und mit einem Pfeil, der die Richtung angibt. Die Richtung des Vektors verläuft von seinem Schwanz zu seinem Kopf.
Wie untersucht man Vektoren?
Sie können die Größe eines Vektors in drei Dimensionen finden, indem Sie die Formel a2=b2+c2+d2 verwenden, wobei a die Größe des Vektors ist und b, c und d die Komponenten in jeder Richtung sind. Das Kreuzprodukt von Vektoren ist nicht kommutativ. Kollineare Vektoren sind auch parallele Vektoren, außer dass sie auf derselben Linie liegen.
Warum untersuchen wir Vektoren?
Die Untersuchung von Vektoren ist wichtig, da sie viele reale Anwendungen hat. Wir wissen, dass Vektoren sowohl Betrag als auch Richtung haben. Daher wird es in der Physik verwendet, um physikalische Größen darzustellen. Es hat viele Anwendungen in der Physik, um Kraft, Geschwindigkeit, Beschleunigung, Verschiebung usw. zu berechnen.
Ist ein Vektor eine Linie?
Vektoren sind keine Linien und haben eine ganz andere Funktion als Linien. Ein Vektor ist eine Richtung und eine Größe, das war’s. Es kann auch „größenlos“ gemacht werden, indem es vereinheitlicht wird (siehe Vicentes Antwort auf Ihre andere Frage). Eine Linie hat natürlich Richtung und Größe, aber sie hat auch ORT.
Was sind Vektoren in der Mathematik?
Vektor, in der Mathematik eine Größe, die sowohl Größe als auch Richtung, aber keine Position hat. Beispiele für solche Größen sind Geschwindigkeit und Beschleunigung.
Ist 3D-Geometrie einfach?
Abstand zwischen zwei Punkten in 3D Der Abstand zwischen zwei Punkten in 2D ist einfach. Aber wenn es um 3D-Geometrie geht, wird es etwas schwierig.
Was ist ein Vektorbeispiel?
Ein Vektor ist eine Größe oder ein Phänomen, das zwei unabhängige Eigenschaften hat: Größe und Richtung. Der Begriff bezeichnet auch die mathematische oder geometrische Darstellung einer solchen Größe. Beispiele für Vektoren
Erklärung: Um den Richtungsvektor zu finden, subtrahieren Sie die Koordinaten des Anfangspunkts von den Koordinaten des Endpunkts. Um einen Einheitsvektor mit der gleichen Richtung wie ein gegebener Vektor zu finden, teilen wir den Vektor durch seine Größe. Stellen Sie sich zum Beispiel einen Vektor v = (1, 4) vor, der eine Größe von hatin der Natur sind Geschwindigkeit, Impuls, Kraft, elektromagnetische Felder und Gewicht.
Was sind Vektoren an einem Beispiel erklären?
Ein Vektor ist ein lebender Organismus, der einen Infektionserreger von einem infizierten Tier auf einen Menschen oder ein anderes Tier überträgt. Vektoren sind häufig Arthropoden wie Mücken, Zecken, Fliegen, Flöhe und Läuse.
Sind Zahlen Vektoren?
Da R ein Vektorraum über sich selbst ist, sind reelle Zahlen in diesem Zusammenhang sowohl Vektoren als auch Skalare. In anderen Kontexten kann eine reelle Zahl ein Vektor sein, aber kein Skalar (z. B. der Vektor √2 in R über Q), ein Skalar, aber kein Vektor (z. B. der Skalar 1 in R2 über R) oder weder ein Vektor noch a Skalar.
Was ist die Vektorform einer Formel?
Die Vektorgleichung einer Linie hat die Form = 0 + t, wobei 0 der Positionsvektor eines bestimmten Punktes auf der Linie ist, t ein Skalarparameter ist, ein Vektor ist, der die Richtung der Linie beschreibt, und der Positionsvektor des Punktes auf der Linie ist, der dem Wert von t.
entspricht
Was ist eine Vektorstruktur?
Ein Vektor ist beim Rechnen im Allgemeinen ein eindimensionales Array, das typischerweise Zahlen speichert. Vektoren haben im Gegensatz zu Listen und Warteschlangen normalerweise feste Größen. Die Vektordatenstruktur kann verwendet werden, um den mathematischen Vektor darzustellen, der in der linearen Algebra verwendet wird.
Wie findet man einen Vektor mit gleicher Richtung?
Um einen Einheitsvektor mit der gleichen Richtung wie ein gegebener Vektor zu finden, teilen wir den Vektor durch seine Größe. Stellen Sie sich zum Beispiel einen Vektor v = (1, 4) vor, der eine Größe von hatRichtung als gegebenen Vektor teilen wir den Vektor durch seine Größe. Stellen Sie sich zum Beispiel einen Vektor v = (1, 4) vor, der eine Größe von hat