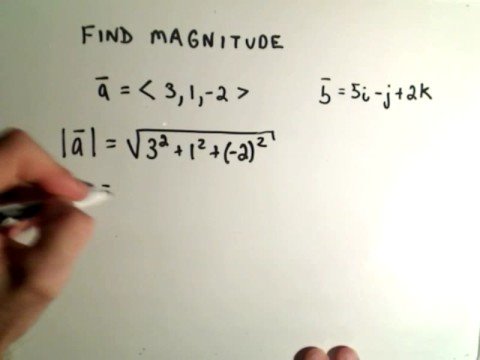plus facile à appliquer que la géométrie et nécessite la connaissance de moins de règles. La mécanique de l’algèbre vectorielle est simple, nécessitant moins d’intuition et d’intelligence pour trouver une solution.
Que signifie l’algèbre vectorielle ?
: une algèbre pour laquelle les éléments impliqués peuvent représenter des vecteurs et les hypothèses et règles sont basées sur le comportement des vecteurs.
Qu’est-ce qu’un vecteur en mathématiques ?
vecteur, en mathématiques, une quantité qui a à la fois une amplitude et une direction mais pas de position. Des exemples de telles grandeurs sont la vitesse et l’accélération.
Comment écrivez-vous un vecteur ?
Lorsqu’un vecteur n’est qu’une liste de nombres, nous pouvons le visualiser comme une flèche dans l’espace. Par exemple, on visualise le vecteur (4,2)left parenthesis, 4, comma, 2, right parenthesis comme une flèche dont la queue est à l’origine et dont la pointe est au point ( 4 , 2 ) (4, 2) ( 4,2) parenthèse gauche, 4, virgule, 2, parenthèse droite.
Comment étudiez-vous les vecteurs ?
Vous pouvez trouver la magnitude d’un vecteur en trois dimensions en utilisant la formule a2=b2+c2+d2, où a est la magnitude du vecteur, et b, c et d sont les composantes dans chaque direction. Le produit croisé des vecteurs n’est pas commutatif. Les vecteurs colinéaires sont également des vecteurs parallèles, sauf qu’ils se trouvent sur la même ligne.
Comment écrivez-vous un vecteur ?
Lorsqu’un vecteur n’est qu’une liste de nombres, nous pouvons le visualiser comme une flèche dans l’espace. Par exemple, on visualise le vecteur (4,2)left parenthesis, 4, comma, 2, right parenthesis comme une flèche dont la queue est à l’origine et dont la pointe est au point ( 4 , 2 ) (4, 2) ( 4,2) parenthèse gauche, 4, virgule, 2, parenthèse droite.
A quoi ressemble un vecteur ?
Définition d’un vecteur. Un vecteur est un objet qui a à la fois une magnitude et une direction. Géométriquement, nous pouvons imaginer un vecteur comme une directionsegment de droite, dont la longueur est la grandeur du vecteur et avec une flèche indiquant la direction. La direction du vecteur va de sa queue à sa tête.
Comment étudiez-vous les vecteurs ?
Vous pouvez trouver la magnitude d’un vecteur en trois dimensions en utilisant la formule a2=b2+c2+d2, où a est la magnitude du vecteur, et b, c et d sont les composantes dans chaque direction. Le produit croisé des vecteurs n’est pas commutatif. Les vecteurs colinéaires sont également des vecteurs parallèles, sauf qu’ils se trouvent sur la même ligne.
Pourquoi étudions-nous les vecteurs ?
L’étude des vecteurs est importante, car elle a de nombreuses applications réelles. Nous savons que les vecteurs ont à la fois une magnitude et une direction. Par conséquent, il est utilisé en physique pour représenter des grandeurs physiques. Il a de nombreuses applications en physique pour calculer la force, la vitesse, l’accélération, le déplacement, etc.
Est-ce qu’un vecteur est une droite ?
Les vecteurs ne sont pas des lignes et ils ont une fonction très différente de celle des lignes. Un vecteur est une direction et une magnitude, c’est tout. Il peut également être rendu « sans magnitude » en étant unifié (voir la réponse de Vicente à votre autre question). Une ligne, bien sûr, a une direction et une magnitude, mais elle a aussi un EMPLACEMENT.
Que sont les vecteurs en mathématiques ?
vecteur, en mathématiques, une quantité qui a à la fois une amplitude et une direction mais pas de position. Des exemples de telles grandeurs sont la vitesse et l’accélération.
La géométrie 3D est-elle facile ?
Distance entre deux points en 3D La distance entre deux points en 2D est simple. Mais, quand il s’agit de géométrie 3D, les choses deviennent un peu difficiles.
Qu’est-ce qu’un exemple de vecteur ?
Un vecteur est une quantité ou un phénomène qui possède deux propriétés indépendantes : l’amplitude et la direction. Le terme désigne également la représentation mathématique ou géométrique d’une telle grandeur. Exemples de vecteurs
Explication : Pour trouver le vecteur directionnel, soustrayez les coordonnées du point initial aux coordonnées du point terminal. Pour trouver un vecteur unitaire ayant la même direction qu’un vecteur donné, nous divisons le vecteur par sa magnitude. Par exemple, considérons un vecteur v = (1, 4) qui a une magnitude dedans la nature sont la vitesse, la quantité de mouvement, la force, les champs électromagnétiques et le poids.
Qu’est-ce que les vecteurs expliquent avec un exemple ?
Un vecteur est un organisme vivant qui transmet un agent infectieux d’un animal infecté à un humain ou à un autre animal. Les vecteurs sont souvent des arthropodes, comme les moustiques, les tiques, les mouches, les puces et les poux.
Les nombres sont-ils des vecteurs ?
Puisque R est un espace vectoriel sur lui-même, les nombres réels sont à la fois des vecteurs et des scalaires dans ce contexte. Dans d’autres contextes, un nombre réel peut être un vecteur mais pas un scalaire (par exemple le vecteur √2 dans R sur Q), un scalaire mais pas un vecteur (par exemple le scalaire 1 dans R2 sur R), ou ni un vecteur ni un scalaire.
Qu’est-ce que la forme vectorielle d’une formule ?
L’équation vectorielle d’une ligne est de la forme = 0 + t, où 0 est le vecteur de position d’un point particulier sur la ligne, t est un paramètre scalaire, est un vecteur qui décrit la direction de la ligne, et est le vecteur position du point sur la droite correspondant à la valeur de t.
Qu’est-ce qu’une structure vectorielle ?
Un vecteur, en informatique, est généralement un tableau unidimensionnel, stockant généralement des nombres. Les vecteurs ont généralement des tailles fixes, contrairement aux listes et aux files d’attente. La structure de données vectorielles peut être utilisée pour représenter le vecteur mathématique utilisé en algèbre linéaire.
Comment trouve-t-on un vecteur de même direction ?
Pour trouver un vecteur unitaire avec la même direction qu’un vecteur donné, nous divisons le vecteur par sa magnitude. Par exemple, considérons un vecteur v = (1, 4) qui a une magnitude dedirection comme un vecteur donné, nous divisons le vecteur par sa grandeur. Par exemple, considérons un vecteur v = (1, 4) qui a une magnitude de