fonction, en mathématiques, une expression, une règle ou une loi qui définit une relation entre une variable (la variable indépendante) et une autre variable (la variable dépendante).
Qu’est-ce qu’une fonction en mathématiques ?
fonction, en mathématiques, une expression, une règle ou une loi qui définit une relation entre une variable (la variable indépendante) et une autre variable (la variable dépendante).
Qu’est-ce qu’une fonction en définition simple ?
Une fonction est définie comme une relation entre un ensemble d’entrées ayant chacune une sortie. En termes simples, une fonction est une relation entre des entrées où chaque entrée est liée à exactement une sortie. Chaque fonction a un domaine et un codomaine ou une plage.
QU’EST-CE QUE la fonction et l’exemple ?
Une fonction est une sorte de règle qui, pour une entrée, vous donne une sortie. Source de l’image : par Alex Federspiel. Un exemple de ceci serait y=x2. Si vous mettez quelque chose pour x, vous obtenez une sortie pour y. Nous dirions que y est une fonction de x puisque x est la valeur d’entrée.
Que sont les fonctions en algèbre ?
Une fonction relie une entrée à une sortie. C’est comme une machine qui a une entrée et une sortie. Et la sortie est en quelque sorte liée à l’entrée. f(x) « f(x) = … » est la manière classique d’écrire une fonction.
Qu’est-ce qu’une fonction en mathématiques ?
fonction, en mathématiques, une expression, une règle ou une loi qui définit une relation entre une variable (la variable indépendante) et une autre variable (la variable dépendante).
Qu’est-ce qu’une fonction en définition simple ?
Une fonction est définie comme une relation entre un ensemble d’entrées ayant chacune une sortie. En termes simples, une fonction est une relation entre des entrées où chaque entrée est liée à exactement une sortie. Chaque fonction a un domaine et un codomaine ou une plage.
Que sontfonctions en algèbre ?
Une fonction relie une entrée à une sortie. C’est comme une machine qui a une entrée et une sortie. Et la sortie est en quelque sorte liée à l’entrée. f(x) « f(x) = … » est la manière classique d’écrire une fonction.
Comment identifiez-vous qu’il s’agit d’une fonction ?
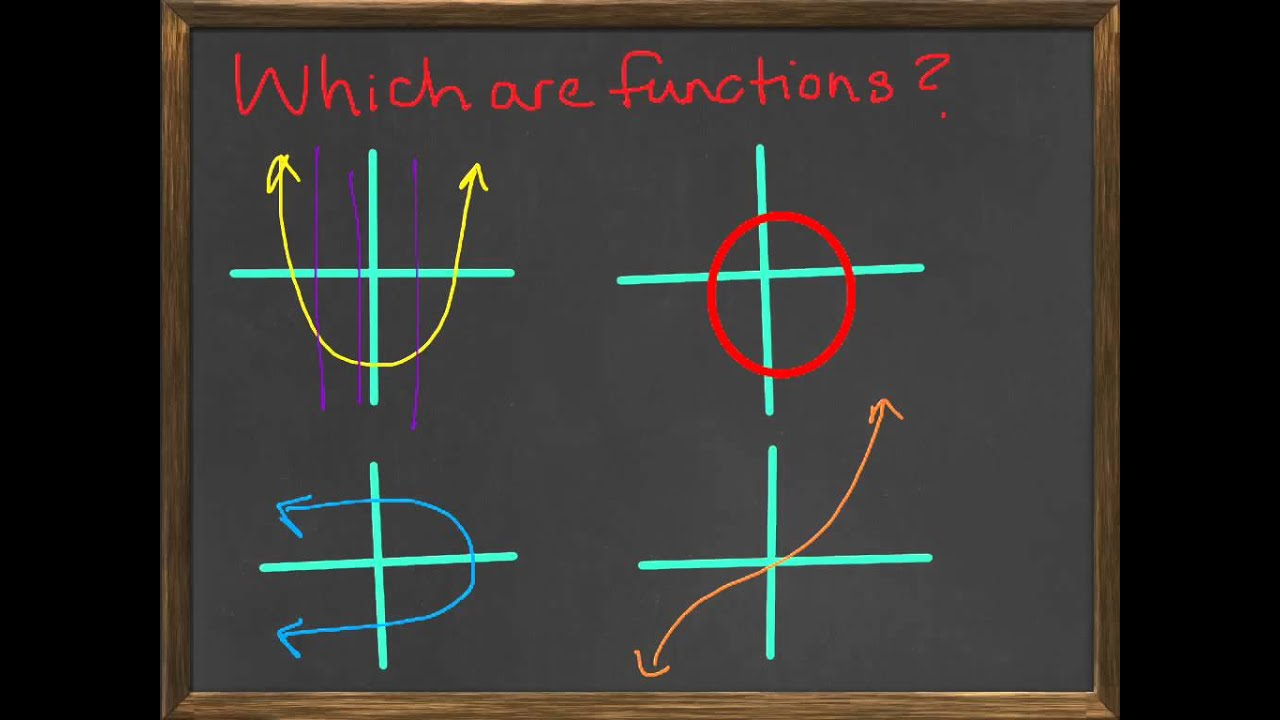
Inspectez le graphique pour voir si une ligne verticale tracée croiserait la courbe plus d’une fois. S’il existe une telle ligne, le graphique ne représente pas une fonction. Si aucune ligne verticale ne peut croiser la courbe plus d’une fois, le graphique représente une fonction.
Comment savez-vous si c’est une fonction ?
Utilisez le test de la ligne verticale pour déterminer si un graphique représente ou non une fonction. Si une ligne verticale est déplacée sur le graphique et, à tout moment, touche le graphique en un seul point, alors le graphique est une fonction. Si la ligne verticale touche le graphique en plus d’un point, alors le graphique n’est pas une fonction.
Qu’est-ce qui n’est pas une fonction ?
Les lignes verticales ne sont pas des fonctions. Les équations y = ± x et x 2 + y 2 = 9 sont des exemples de non-fonctions car il existe au moins une -valeur avec deux ou plusieurs -valeurs.
Quels sont les 3 types de fonctions ?
Types de fonctions Plusieurs – une fonction. Onto – fonction (fonction surjective) Into – fonction. Fonction polynomiale.
Quelle équation n’est pas une fonction ?
Les lignes verticales ne sont pas des fonctions. Les équations y = ± x et x 2 + y 2 = 9 sont des exemples de non-fonctions car il existe au moins une -valeur avec deux ou plusieurs -valeurs.
Quelle est la différence entre une fonction et une équation ?
Une fonction a au moins 2 variables : une variable de sortie et une ou plusieurs variables d’entrée. Une équation indique que deux expressions sont égales et peut impliquer n’importe quel nombre de variables (aucune, une ou plusieurs). Une fonction peut souvent être écrite sous la forme d’unéquation, mais toutes les équations ne sont pas des fonctions.
Quelle est la meilleure définition de fonction ?
Une définition technique d’une fonction est : une relation entre un ensemble d’entrées et un ensemble de sorties possibles où chaque entrée est liée à exactement une sortie.
Qu’est-ce qu’une définition de fonction pour les enfants ?
fonction. • une relation mathématique entre un ensemble d’entrées et un ensemble de sorties. • la valeur de sortie dépend de (est une fonction de) la valeur d’entrée. et chaque entrée produit exactement une sortie.
Qu’est-ce qu’une fonction en mathématiques ?
fonction, en mathématiques, une expression, une règle ou une loi qui définit une relation entre une variable (la variable indépendante) et une autre variable (la variable dépendante).
Qu’est-ce qu’une fonction en définition simple ?
Une fonction est définie comme une relation entre un ensemble d’entrées ayant chacune une sortie. En termes simples, une fonction est une relation entre des entrées où chaque entrée est liée à exactement une sortie. Chaque fonction a un domaine et un codomaine ou une plage.
Que sont les fonctions en algèbre ?
Une fonction relie une entrée à une sortie. C’est comme une machine qui a une entrée et une sortie. Et la sortie est en quelque sorte liée à l’entrée. f(x) « f(x) = … » est la manière classique d’écrire une fonction.
Pourquoi est-ce une fonction ?
Une fonction est une relation dans laquelle chaque entrée n’a qu’une seule sortie. Dans la relation , y est une fonction de x, car pour chaque entrée x (1, 2, 3 ou 0), il n’y a qu’une seule sortie y. x n’est pas une fonction de y, car l’entrée y = 3 a plusieurs sorties : x = 1 et x = 2.
QU’EST-CE QUE la fonction et la non-fonction ?
Quelle est la différence entre les exigences fonctionnelles et non fonctionnelles ? Les exigences fonctionnelles expliquent comment le système doit fonctionner, tandis que les exigences non fonctionnelles expliquent comment le systèmedevrait fonctionner.
Combien y a-t-il de types de fonctions ?
Les types de fonctions peuvent être globalement classés en quatre types. Basé sur l’élément : une à une fonction, plusieurs à une fonction, sur une fonction, une à une et sur une fonction, dans une fonction. Basé sur le domaine : fonctions algébriques, fonctions trigonométriques, fonctions logarithmiques.