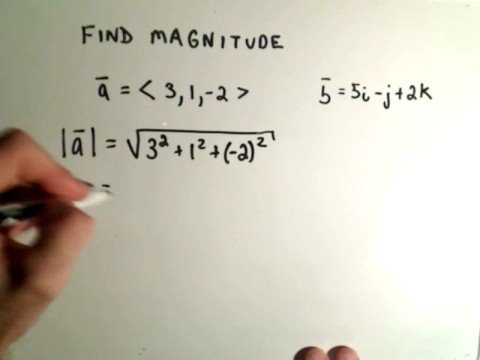Explanation: To find the directional vector, subtract the coordinates of the initial point from the coordinates of the terminal point.To find a unit vector with the same direction as a given vector, we divide the vector by its magnitude. For example, consider a vector v = (1, 4) which has a magnitude of |v|. If we divide each component of vector v by |v| we will get the unit vector u v which is in the same direction as v.
What is vector rule?
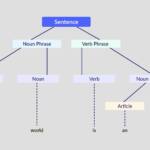
Two vectors are equal only if they have the same magnitude and direction. This condition can be described mathematically as follows: Vector is equal to vector only when. 5. When two or more vectors are added together, the resulting vector is called the resultant.
What is vector method?
Vector implements a dynamic array which can hold the array of any type and any number. It is similar to ArrayList, but with two differences: 1) Vector is synchronized. 2) it contains many legacy methods that are not part of the collections framework. These objects do not have to be homogenous.
What is a vector example?
A vector is a quantity or phenomenon that has two independent properties: magnitude and direction. The term also denotes the mathematical or geometrical representation of such a quantity. Examples of vectors in nature are velocity, momentum, force, electromagnetic fields, and weight.
How do you do vectors in maths?
The vector can also be represented by the column vector . The top number tells you how many spaces or units to move in the positive -direction and the bottom number is how many to move in the positive -direction. Vectors are equal if they have the same magnitude and direction regardless of where they are.
Is vector algebra easy?
Vector algebra is much easier to apply than geometry and requires knowledge of fewer rules. The mechanics of vector algebra are straightforward, requiring less intuition and cleverness in finding a solution.
What is vector algebra means?
: an algebra for which the elements involved may represent vectors and the assumptions and rules are based on the behavior of vectors.
What is a vector in math?
vector, in mathematics, a quantity that has both magnitude and direction but not position. Examples of such quantities are velocity and acceleration.
How do you write a vector?
When a vector is just a list of numbers, we can visualize it as an arrow in space. For example, we visualize the vector (4,2)left parenthesis, 4, comma, 2, right parenthesis as an arrow whose tail is at the origin and whose tip is at the point ( 4 , 2 ) (4, 2) (4,2)left parenthesis, 4, comma, 2, right parenthesis.
How do you study vectors?
You can find the magnitude of a vector in three dimensions by using the formula a2=b2+c2+d2, where a is the magnitude of the vector, and b, c, and d are the components in each direction. Cross product of vectors is not commutative. Collinear Vectors are also parallel vectors except that they lie on the same line.
How do you write a vector?
When a vector is just a list of numbers, we can visualize it as an arrow in space. For example, we visualize the vector (4,2)left parenthesis, 4, comma, 2, right parenthesis as an arrow whose tail is at the origin and whose tip is at the point ( 4 , 2 ) (4, 2) (4,2)left parenthesis, 4, comma, 2, right parenthesis.
What does a vector look like?
Definition of a vector. A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.
How do you study vectors?
You can find the magnitude of a vector in three dimensions by using the formula a2=b2+c2+d2, where a is the magnitude of the vector, and b, c, and d are the components in each direction. Cross product of vectors is not commutative. Collinear Vectors are also parallel vectors except that they lie on the same line.
Why do we study vectors?
The study of vectors is important, as it has many real-life applications. We know that vectors have both magnitude and direction. Hence, it is used in Physics to represent physical quantities. It has many applications in Physics to calculate force, velocity, acceleration, displacement, and so on.
Is a vector a line?
Vectors are not lines and they have a very different function than lines. A vector is a direction and a magnitude, that’s it. It can also be made “magnitudeless” by being unitized (see Vicente’s response to your other question). A line, of course, has direction and magnitude, but it also has LOCATION.
What are vectors in maths?
vector, in mathematics, a quantity that has both magnitude and direction but not position. Examples of such quantities are velocity and acceleration.
Is 3D geometry easy?
Distance between two points in 3D Distance between two points in 2D is simple. But, when it comes to 3D geometry, things become a little difficult.
What is a vector example?
A vector is a quantity or phenomenon that has two independent properties: magnitude and direction. The term also denotes the mathematical or geometrical representation of such a quantity. Examples of vectors in nature are velocity, momentum, force, electromagnetic fields, and weight.
What are vectors explain with an example?
A vector is a living organism that transmits an infectious agent from an infected animal to a human or another animal. Vectors are frequently arthropods, such as mosquitoes, ticks, flies, fleas and lice.
Are numbers vectors?
Since R is a vector space over itself, real numbers are both vectors and scalars in this context. In other contexts, a real number might be a vector but not a scalar (e.g. the vector √2 in R over Q), a scalar but not a vector (e.g. the scalar 1 in R2 over R), or neither a vector nor a scalar.
What is vector form of a formula?
The vector equation of a line is of the form = 0 + t, where 0 is the position vector of a particular point on the line, t is a scalar parameter, is a vector that describes the direction of the line, and is the position vector of the point on the line corresponding to the value of t.
What is a vector structure?
A vector, in computing, is generally a one-dimensional array, typically storing numbers. Vectors typically have fixed sizes, unlike lists and queues. The vector data structure can be used to represent the mathematical vector used in linear algebra.
How do you find a vector with the same direction?
To find a unit vector with the same direction as a given vector, we divide the vector by its magnitude. For example, consider a vector v = (1, 4) which has a magnitude of |v|. If we divide each component of vector v by |v| we will get the unit vector u v which is in the same direction as v. How to represent Vector in a bracket format?
How to find the unit vector of a vector?
How to find the unit vector? To find a unit vector with the same direction as a given vector, we divide the vector by its magnitude. For example, consider a vector v = (1, 4) which has a magnitude of |v|. If we divide each component of vector v by |v| we will get the unit vector u v which is in the same direction as v.
How do you find the components of a vector?
The components of a vector give a split of the vector. The vector is split according to each of the axes and we can calculate the components of a vector. Any vector in a two-dimensional coordinate system can be broken down into its \ (x\) and \ (y\)-components.
How to find the direction of a vector with endpoints?
To find the direction of a vector whose endpoints are given by the position vectors (x 1, y 1) and (x 2, y 2 ), then to find its direction: Find the vector (x, y) using the formula (x, y) = (x 2 – x 1, y 2 – y 1)