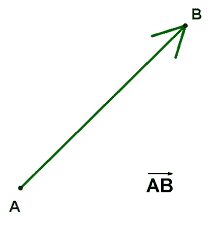
Το διάνυσμα και η ακτίνα συμβολίζονται με τον ίδιο τρόπο: ένα ευθύγραμμο τμήμα με ένα βέλος στο ένα άκρο αλλά είναι πολύ διαφορετικά πράγματα. Ένα διάνυσμα έχει κατεύθυνση και μέγεθος (για παράδειγμα, 5 km νοτιοανατολικά). Μια ακτίνα έχει απλώς μια κατεύθυνση και ένα σημείο εκκίνησης και έχει άπειρο μήκος. Το διάνυσμα και η ακτίνα συμβολίζονται με τον ίδιο τρόπο: ένα ευθύγραμμο τμήμα με ένα βέλος στο ένα άκρο, αλλά είναι πολύ διαφορετικά πράγματα. Ένα διάνυσμα έχει κατεύθυνση και μέγεθος (για παράδειγμα, 5 km νοτιοανατολικά). Το διάνυσμα είναι έτσι: Μια ακτίνα έχει απλώς μια κατεύθυνση και ένα σημείο εκκίνησης και έχει άπειρο μήκος.
Πώς ορίζεις μια ακτίνα;
1 : μία από τις γραμμές φωτός που φαίνεται να ακτινοβολεί από ένα φωτεινό αντικείμενο. 2 : δέσμη ακτινοβολούμενης ενέργειας (ως φως) μικρής διατομής. 3α : ένα ρεύμα σωματιδίων υλικού που ταξιδεύουν στην ίδια γραμμή (όπως στα ραδιενεργά φαινόμενα) β : ένα μόνο σωματίδιο ενός τέτοιου ρεύματος. Άλλα λόγια από ακτίνα.
Τι είναι η ακτίνα στα μαθηματικά παραδείγματα;
Στη γεωμετρία, μια ακτίνα είναι μια ευθεία με ένα μόνο τελικό σημείο (ή σημείο προέλευσης) που εκτείνεται άπειρα προς μία κατεύθυνση. Ένα παράδειγμα ακτίνας είναι μια ηλιακή ακτίνα στο διάστημα. ο ήλιος είναι το τελικό σημείο και η ακτίνα του φωτός συνεχίζει απεριόριστα.
Ποια είναι η διαφορά μεταξύ μιας γραμμής και ενός διανύσματος;
Μια γραμμή έχει μια σταθερή θέση στον τρισδιάστατο χώρο. Ένα διάνυσμα δείχνει μόνο μια κατεύθυνση και ένα μέγεθος, όχι μια θέση. Όσον αφορά τα δεδομένα που πραγματικά αποθηκεύονται, καθώς ένα διάνυσμα υποδεικνύει μόνο την κατεύθυνση και το μέγεθος, υποθέστε ότι το σημείο έναρξης είναι (0,0,0), το διάνυσμα αποθηκεύει μόνο το τελικό σημείο.
Ποια είναι η διαφορά μεταξύ ακτίνας και γραμμής;
Μια γραμμή είναι μια ευθεία διαδρομή σε ένα επίπεδο που εκτείνεται για πάντα και προς τις δύο κατευθύνσεις χωρίς τελικά σημεία. Ένα ευθύγραμμο τμήμα είναι μέρος μιας ευθείας που έχει δύο τελικά σημεία και είναι πεπερασμένο σε μήκος. Μια ακτίνα είναι ένα ευθύγραμμο τμήμα που εκτείνεταιεπ’ αόριστον προς μία κατεύθυνση.
Πόσες ακτίνες υπάρχουν;
Έτσι υπάρχουν 8 ακτίνες. Σημείωση: Γνωρίζουμε ότι μια ευθεία είναι ένα βασικό γεωμετρικό σχήμα που αποτελείται από σημεία και εκτείνεται σε δύο κατευθύνσεις. Μια ακτίνα είναι μέρος της ευθείας γραμμής αλλά εκτείνεται μόνο προς μία κατεύθυνση.
Γιατί μια ακτίνα είναι καθορισμένος όρος;
Ο ορισμός της ακτίνας στα μαθηματικά είναι ότι είναι μέρος μιας γραμμής που έχει σταθερό σημείο εκκίνησης αλλά όχι τελικό σημείο. Μπορεί να εκτείνεται άπειρα προς μία κατεύθυνση. Δεδομένου ότι μια ακτίνα δεν έχει τελικό σημείο, δεν μπορούμε να μετρήσουμε το μήκος της. Διασκεδαστικά γεγονότα: Οι ακτίνες του ήλιου είναι ένα παράδειγμα ακτίνας.
Τι είναι η ακτίνα μαθηματικών 4ης τάξης;
Η ακτίνα είναι μια ευθεία σειρά σημείων που ξεκινά από ένα σημείο και συνεχίζεται για πάντα προς μία κατεύθυνση. Η ακτίνα ΑΒ γράφεται ως ΑΒ. Μια γωνία αποτελείται από ακτίνες, ευθείες ή ευθύγραμμα τμήματα που συναντώνται σε ένα κοινό σημείο. Η γωνία που εμφανίζεται στα δεξιά μπορεί να ονομαστεί A, CAB ή BAC.
Μπορεί μια ακτίνα να έχει 3 σημεία;
Ονομασία ακτίνων Μια ακτίνα έχει μια κατευθυντική συνιστώσα, επομένως προσέξτε πώς την ονομάζετε. Η ακτίνα ΑΒ δεν είναι ίδια με την ακτίνα ΒΑ. Μια ακτίνα με 3 σημειωμένα σημεία μπορεί να ονομαστεί με διαφορετικούς τρόπους, όπως φαίνεται παρακάτω. Απλώς φροντίστε να συμπεριλάβετε το τελικό σημείο.
Πώς μοιάζει μια διανυσματική εξίσωση;
Η διανυσματική εξίσωση μιας γραμμής είναι της μορφής = 0 + t, όπου 0 είναι το διάνυσμα θέσης ενός συγκεκριμένου σημείου στη γραμμή, t είναι μια βαθμωτή παράμετρος, είναι ένα διάνυσμα που περιγράφει την κατεύθυνση της γραμμής, και είναι το διάνυσμα θέσης του σημείου της ευθείας που αντιστοιχεί στην τιμή του t.
Ποια είναι η διαφορά μεταξύ ενός διανύσματος και ενός σημείου;
Ένα σημείο έχει θέση στο διάστημα. Το μόνο χαρακτηριστικό που ξεχωρίζει το ένα σημείο από το άλλο είναι η θέση του. Ένα Διάνυσμα έχει και μέγεθος και κατεύθυνση, αλλά δεν έχει σταθερή θέση στο χώρο. Γεωμετρικά, σχεδιάζουμε σημεία ως τελείες και διανύσματα ως ευθείατμήματα με βέλη.
Πώς προσδιορίσατε μια ακτίνα;
Μια ακτίνα είναι ένα μέρος μιας γραμμής που έχει ένα τελικό σημείο και συνεχίζεται άπειρα μόνο προς μία κατεύθυνση. Δεν μπορείτε να μετρήσετε το μήκος μιας ακτίνας. Μια ακτίνα ονομάζεται χρησιμοποιώντας πρώτα το τελικό της σημείο και μετά οποιοδήποτε άλλο σημείο της ακτίνας (για παράδειγμα, →BA ).
Πόσα σημεία είναι μια ακτίνα;
Μια ακτίνα ξεκινά από ένα σημείο και εκτείνεται άπειρα προς μία κατεύθυνση. Άρα, έχει ένα τελικό σημείο.
Ποιος είναι ο ορισμός ενός κουίζλετ ακτίνων;
Ακτίνα. Ένα μέρος μιας γραμμής – έχει ένα τελικό σημείο και συνεχίζει και συνεχίζει προς μία μόνο κατεύθυνση. Γωνία. Σχηματίζεται από δύο ακτίνες που έχουν το ίδιο τελικό σημείο.
Τι είναι η ακτίνα στα μαθηματικά της 4ης τάξης;
Η ακτίνα είναι μια ευθεία σειρά σημείων που ξεκινά από ένα σημείο και συνεχίζεται για πάντα προς μία κατεύθυνση. Η ακτίνα ΑΒ γράφεται ως ΑΒ. Μια γωνία αποτελείται από ακτίνες, ευθείες ή ευθύγραμμα τμήματα που συναντώνται σε ένα κοινό σημείο.
Πώς βρίσκετε μια ακτίνα στη γεωμετρία;
Επεξήγηση: Οι δύο πλευρές μιας γωνίας είναι οι δύο ακτίνες που τη συνθέτουν. Κάθε μία από αυτές τις ακτίνες ξεκινά από την κορυφή και προχωρά από εκεί. Κατά την ονομασία μιας ακτίνας, ξεκινάμε πάντα με το γράμμα του τελικού σημείου (από όπου ξεκινά η ακτίνα) ακολουθούμενο από ένα άλλο σημείο στην ακτίνα προς την κατεύθυνση που ταξιδεύει.
Πώς σχεδιάζετε μια ακτίνα;
Για να σχεδιάσετε μια ακτίνα, σχεδιάζετε ένα σημείο και μετά σχεδιάζετε μια ευθεία γραμμή που βγαίνει από αυτήν προς μία κατεύθυνση. Στο τέλος της γραμμής, προσθέτετε ένα σημείο βέλους για να δείξετε ότι συνεχίζεται για πάντα.
Πώς σχεδιάζετε μια ακτίνα;
Για να σχεδιάσετε μια ακτίνα, σχεδιάζετε ένα σημείο και μετά σχεδιάζετε μια ευθεία γραμμή που βγαίνει από αυτήν προς μία κατεύθυνση. Στο τέλος της γραμμής, προσθέτετε ένα σημείο βέλους για να δείξετε ότι συνεχίζεται για πάντα.
Ποιο είναι το αντίθετο των ακτίνων;
Τι είναι μια αντίθετη ακτίνα στη γεωμετρία; Δύο γεωμετρικές ακτίνες που μοιράζονται το ίδιο τελικό σημείο σχηματίζουν μια γωνία μεταξύ τους. Αν αυτές οι γωνίεςμετρούν 180 μοίρες, δείχνουν προς αντίθετες κατευθύνσεις. Αυτές ονομάζονται αντίθετες ακτίνες.
Γιατί το μηδέν είναι φυσικός αριθμός;
Αν και το μηδέν δεν είναι θετικός αριθμός, εξακολουθεί να θεωρείται ακέραιος αριθμός. Η κατάσταση του μηδέν ως ακέραιος αριθμός και το γεγονός ότι δεν είναι αρνητικός τον κάνει να θεωρείται φυσικός αριθμός από ορισμένους μαθηματικούς.
Μια ακτίνα συνεχίζεται για πάντα;
Ένα ευθύγραμμο τμήμα συμβολίζεται με τα δύο τελικά του σημεία, όπως στο . Μια ακτίνα έχει ένα τελικό σημείο και συνεχίζει για πάντα προς μια κατεύθυνση. Οι μαθηματικοί ονομάζουν μια ακτίνα με συμβολισμό όπως , όπου το σημείο Ε είναι το τελικό σημείο και το F είναι ένα σημείο στην ακτίνα. Όταν ονομάζουμε μια ακτίνα, λέμε πάντα πρώτα το τελικό σημείο.
Τι σημαίνει το upside t στα μαθηματικά;
Κάθετες ευθείες είναι ευθείες, τμήματα ή ακτίνες που τέμνονται για να σχηματίσουν ορθές γωνίες. Το σύμβολο ⊥ σημαίνει είναι κάθετο στο .
Ποια είναι η διαφορά μεταξύ ενός διανύσματος και ενός πίνακα;
– Ένα διάνυσμα είναι ένας δυναμικός πίνακας, του οποίου το μέγεθος μπορεί να αυξηθεί, όπου το μέγεθος του πίνακα δεν μπορεί να αλλάξει. – Ο αποθεματικός χώρος μπορεί να δοθεί για διάνυσμα, όπου όπως για τους πίνακες δεν μπορεί. – Διάνυσμα είναι μια κλάση όπου ως πίνακας δεν είναι. – Τα διανύσματα μπορούν να αποθηκεύσουν οποιοδήποτε τύπο αντικειμένων, όπου ως πίνακας μπορούν να αποθηκεύσουν μόνο ομοιογενείς τιμές.
Ποια είναι η διαφορά μεταξύ ενός βαθμωτού και ενός διανύσματος;
Οι βαθμωτές δεν έχουν κατεύθυνση ενώ το διάνυσμα έχει. Λόγω αυτού του χαρακτηριστικού, η κλιμακωτή ποσότητα μπορεί να ειπωθεί ότι αναπαρίσταται μονοδιάστατη ενώ μια διανυσματική ποσότητα μπορεί να είναι πολυδιάστατη. Από τον παρακάτω πίνακα, ας μάθουμε περισσότερες διαφορές μεταξύ βαθμωτών και διανυσμάτων. Δώστε τα δύο παραδείγματα μεγεθών κλιμάκωσης.
Τι είναι το διάνυσμα στα μαθηματικά;
Ένα διάνυσμα είναι ένα συγκεκριμένο στοιχείο σε ένα διανυσματικό χώρο. Σε ένα Χώρο Hilbert για παράδειγμα, ένα διάνυσμα μπορεί να είναι η συνάρτηση Sinc στους πραγματικούς αριθμούς, και αυτό είναιούτε ένα σημείο στο διάστημα, ούτε ένα βέλος που δείχνει κατεύθυνση ή μετατόπιση ή οτιδήποτε άλλο. Είναι απλώς μια αφηρημένη έννοια.
Είναι τα σημεία και τα διανύσματα το ίδιο πράγμα;
Νομίζω ότι αυτή είναι μια πραγματικά καλή εξήγηση του γιατί ένα σημείο και ένα διάνυσμα δεν είναι εννοιολογικά το ίδιο πράγμα. Θα ήταν χρήσιμο να αναφέρετε (αν συμφωνείτε) ότι σε πολλές περιπτώσεις (π.χ. γραφικά υπολογιστή) τα σημεία αναπαρίστανται ως διανύσματα από μια προέλευση. Ο EtherDragon έθιξε αυτό στο δεύτερο σχόλιο. Τα σημεία και τα διανύσματα δεν είναι το ίδιο πράγμα.